用光影打开孩子大脑的几何空间——勾股定理深度应用（空间最短路径）

如何把“两点之间，线段最短“运用到立体表面上，超级课堂带你具体研究下空间最短路径这类问题！

      ▲基础篇▲       

基础例题1

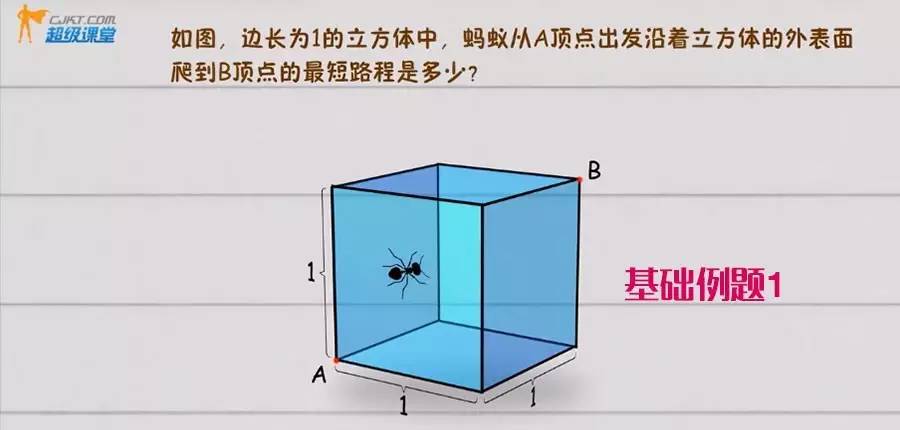
解题思想：把空间问题转化为平面问题

具体操作：将几何体外表面展开

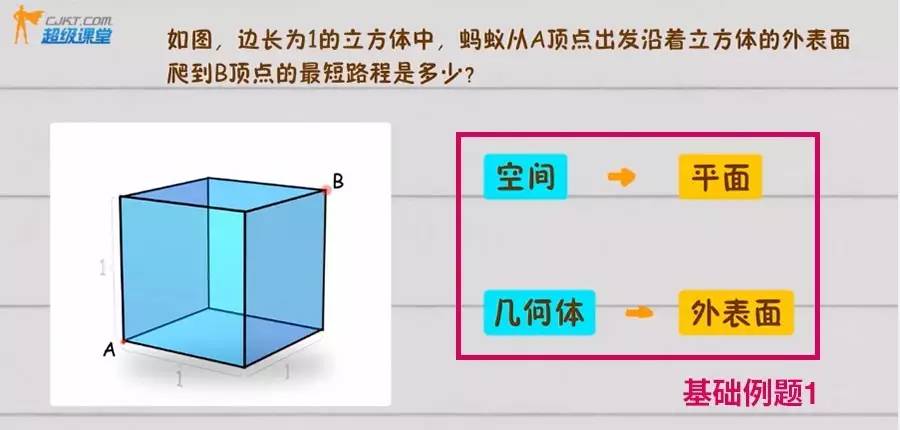
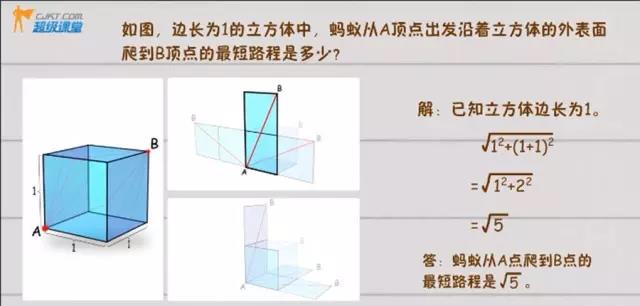
把正方体展开，画出AB点的位置，连接AB，一共有6条路线：

但这6条路线的长度一样，都为矩形的对角线。

利用勾股定理，求解如下：

例题2

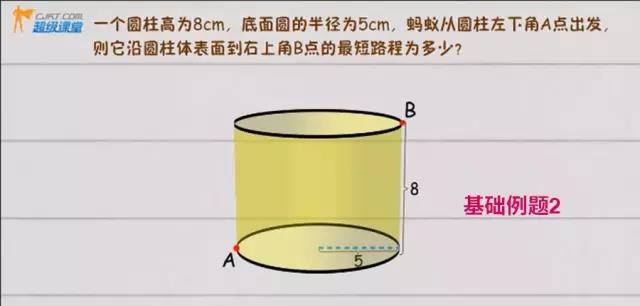
同样将几何体（圆柱）外表面展开，是一个长方形

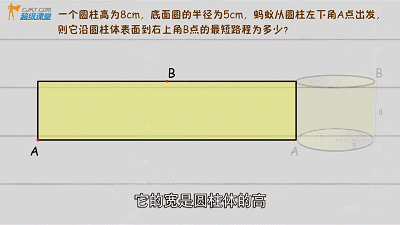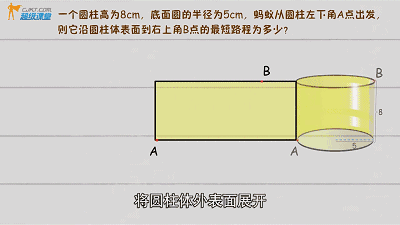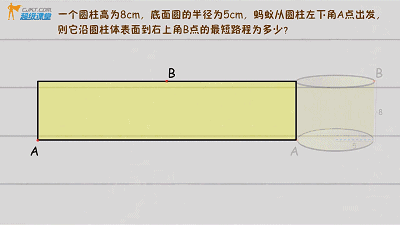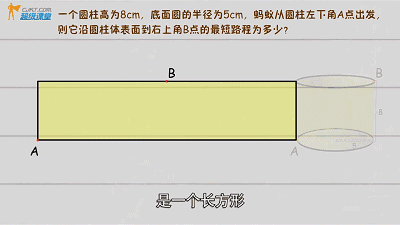
（具体解题查看视频）

■进阶篇■

基础变式

与立方体一样有6种路线，但题目并没有指定路线，而长、宽、高又各不相等，所以6种路线的长度不等。

由于长方体相对的面全等，则把这六种路线分成三类讨论：

1“前上”与“下后”

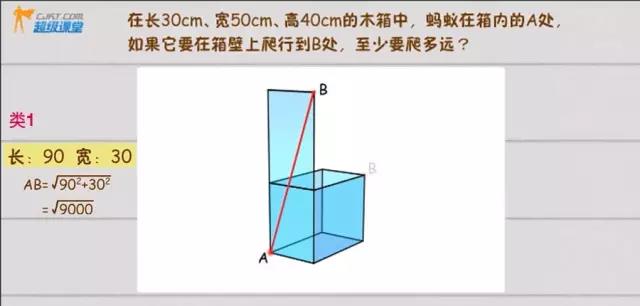
2“前右”与“左后”

3“左上”与“下右”

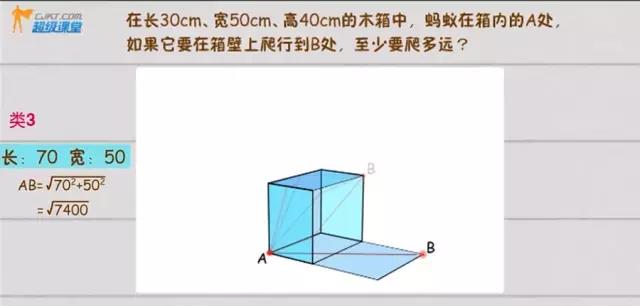
综上，类3的选择的路程最短。

学长笔记：未定路线的长方体表面最短路径问题需分类讨论

       ★进阶篇★       

提高例题1

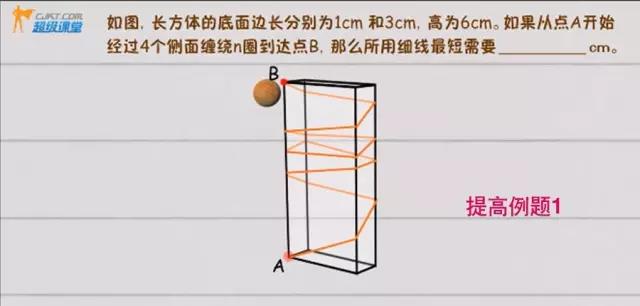
思考，细线总长就是A和B的空间最短路径长度。所以把长方体的侧面展开1次，路线选择为前右后左，则展开图唯一如下：

绕一圈时边长为3+1+3+1，8cm，思考，n圈的展开图如下：

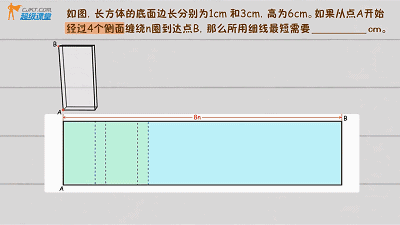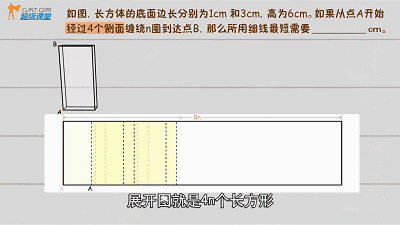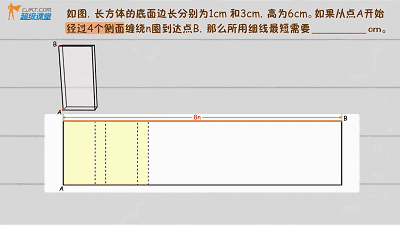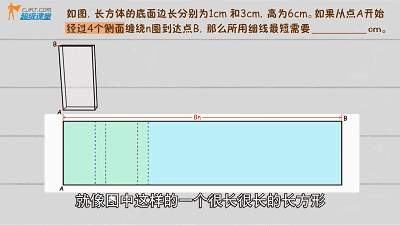
边长分别为8n和6cm，利用勾股定理得：

提高例题2

蚂蚁会经过长方体的三个侧面，把这三个侧面展开：

学长提醒：增加的长度为2个正方形边长，不是3个

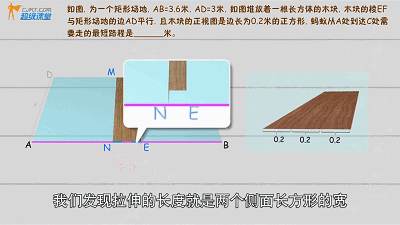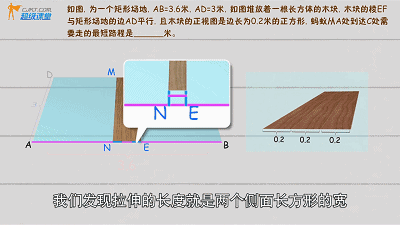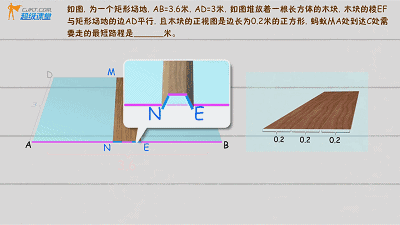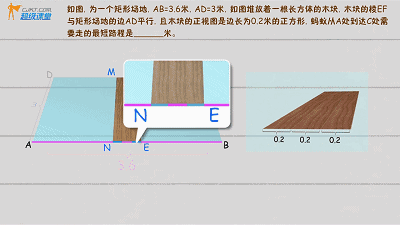
（具体解题查看视频）

学长笔记：平面、空间混合问题同样把几何体表面展开，化空间为平面。

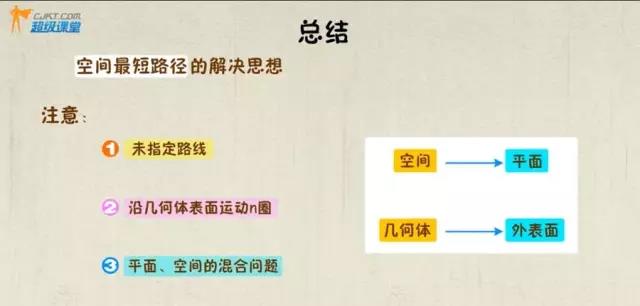
       ●总结●       

1、遇到长方体表面的最短路径问题时，如果题目没有指定路线的选择，要注意分类讨论；

2、如果沿几何体表面运动n圈，相当于经历n次循环，展开图中的长要扩大为n倍；

3、平面、空间的混合问题只需要把经历的几何体表面展开，与平面连接在一起便可以轻松解决。